問題例
N個の品物があります。 品物には1,2,…,Nと番号が振られています。 各i(1≤i≤N) について、品物iの重さはwiで、価値はviです。太郎君は、N個の品物のうちいくつかを選び、ナップサックに入れて持ち帰ることにしました。 ナップサックの容量はWであり、持ち帰る品物の重さの総和はW以下でなければなりません。太郎君が持ち帰る品物の価値の総和の最大値を求めてください。
引用: https://atcoder.jp/contests/dp/tasks/dp_d
考え方
各品物に注目すると、まず品物をいれても重さの上限を超えない場合は(価値は非負なので)必ず入れたほうがよい。
次に、その品物を入れて重さがオーバーしてしまう場合、その荷物1つだけで重さの上限を突破しない限り、"今までに選んだ品物をいくらか捨てて"今の品物を入れるという操作ができる。(もちろん必ず価値が上がるわけではないが)
例えば、重さ上限10, 現時点で選んだ品物の重さの合計が7, 今注目している品物の重さが5とする。この時できる操作は、
・今回の品物は入れない
・品物の重さの合計が5以下になるまで減らして、今回の品物を入れる
となる。前者は単純に価値を足し合わせればよい。では後者の方法で価値を最大化させるにはどうしたらよいか。そこで出てくるのがナップサックDPである。
品物の重さの合計が5以下になるまで減らす、という行為は、予め"i番目までの品物から重さの合計が5以下になるように選んだ時の価値の最大値"を求めておけばよい。
では、この"i番目までの品物から重さの合計が5以下になるように選んだ時の価値の最大値"はどのように求められるか考える。
注目している品物の重さが5より大きい場合、全ての品物を取り出して入れてもオーバーしてしまうため、"i番目までの品物から重さの合計が
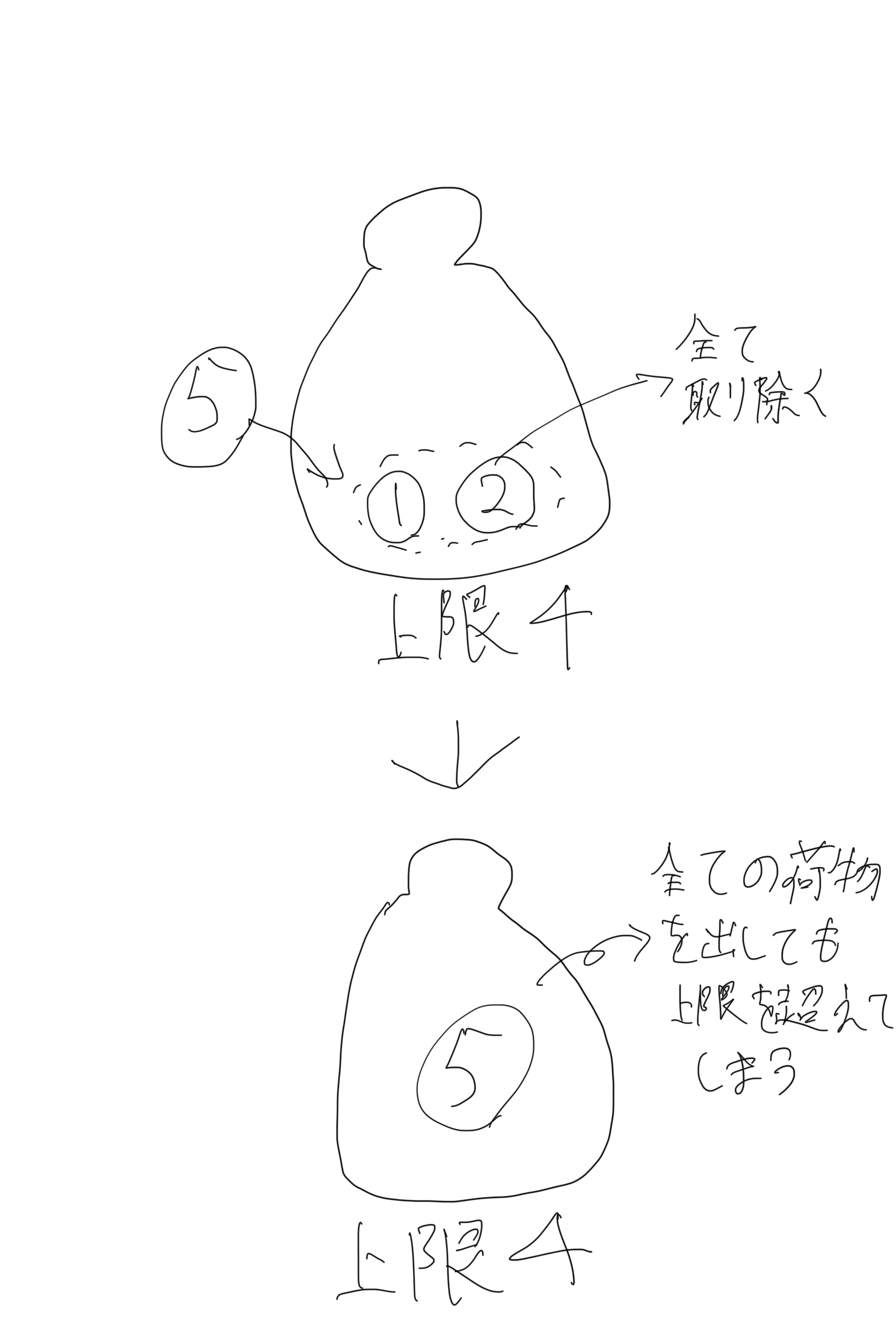
注目している品物の重さが5より小さい場合、
・"i番目までの品物の中から重さが5-[今回の品物の重さ]であるときの価値の最大値"+今回品物の価値
・"i番目までの品物から重さの合計が4以下になるように選んだ時の価値の最大値"
となる。つまり、"1-N番目までの品物を重さ0-W以下になるように選んだ時の価値の最大値"を考えていく、というのが解法であり、
今注目している(i番目とする)品物を入れることができる(今の重さ(jとする)の上限>=今注目している荷物の重さ(wとする))時、最大値は
max(i-1番目までの品物を重さj-w以下になるように選んだときの最大値 + 今回の価値, i-1番目までの品物を重さj以下になるように選んだ時の最大値)
今注目している(i番目とする)品物を入れることができない場合、
i-1番目までの品物を重さj以下になるように選んだ時の最大値(先ほどの図)
となる。
これを二次元配列で dp[i][j](i番目までの品物から重さの合計がj以下になるように選んだ時の価値の最大値)と置いて、要素を更新していく。
一般的には、 dp[i + 1][j] = max(dp[i][j - w[i]] + v[i], dp[i][j]) のように、左辺の添え字にi+1を持ってくる書き方が普通っぽい。
